第3章 学习分类—基于图像大小进行分类

🖼 人工智能学习总目录

🖼《白话机器学习数学》小结及目录

• 第1章 开始二人之旅
• 第2章 学习回归—基于广告费预测点击率
• 第3章 学习分类—基于图像大小进行分类
• 第4章 评估已建立的模型
• 第5章 实现—使用Python编程

本章知识小结：

• 1、内积、权重向量
• 2、感知机、线性可分
• 3、逻辑回归、sigmoid函数、决策边界
• 4、似然函数
• 5、对数似然函数

1、设置问题

把横纵长方形长宽视为坐标记录在坐标轴，在坐标轴划线 进行二分类，线两侧是两种类型（目的是找到线）

2、内积

第二章回归问题是求类似这样的一次函数的斜率和截距

我们这里的目的是找到向量，一次函数是使权重向量成为法线向量的直线（权重向量=法线向量）

设权重向量ω=(1,1)，对于二维的图像来说，对应的直线x可以由下公式求得：

$$\bfω\cdot\bf x = 0 \newline (1,1)\cdot\bf (x_1,x_2) = x_1 + x_2 = 0 \newline x_2 = - x_1$$

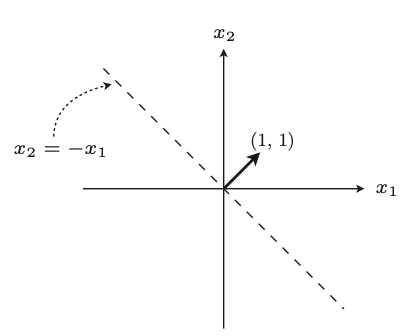
参考下图，我们的目的从求直线的斜率截距变成了通过训练求权重向量，得到垂直直线，再进行分类。

求权重参数的做法和回归时相同，将权重向量用作参数，创建更新表达式来更新参数。

3、感知机（perceptorn）

感知机是接受多个输入后将每个值与各自的权重相乘，最后输出总和的模型。

（只能解决线性可分问题）

（感知机是非常简单的模型，基本不会应用在实际问题中，但是它是神经网络和深度学习的基础模型）

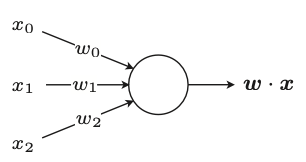
3.1 训练数据的准备

设表示宽的轴为x1，表示长的轴为x2，用y表示图像是横向还是纵向（横向1，纵向-1）

图像大小	形状	x1	x2	y
80x150	纵向	80	150	-1
60x110	纵向	60	110	-1
35x130	纵向	35	130	-1
160x50	横向	160	50	1
160x20	横向	160	20	1
125x30	横向	125	30	1

判别函数：

$$f(x)= \begin{cases} 1&(\bfω\cdot\bf x \ge 0) \\ -1&(\bfω\cdot\bf x < 0) \end{cases}$$

3.2 权重向量的更新表达式

$$ω :=\begin{cases} ω+y^{(i)}x^{(i)}&(f_\bfω(x^{(i)})\ne y^{(i)}) \\ ω&(f_\bfω(x^{(i)})= y^{(i)}) \end{cases}$$

这里的i是训练数据的索引，而不是i次方的意思。

判别函数分类的结果不正确的时候才会进行参数的更新。

这里的更新表达式：

$$\bfω:=\bfω+y^{(i)}x^{(i)}$$

一开始的ω是随机初始化的，如下图我们随机初始化一个ω，判别x=（125,25）形状是纵向（应该是横向，判断错误），更新的过程类似把ω和x向量向加，更新后的w+x明显可以判断出x是横向的，从而达到更好的判断效果的目的。

（也可以理解为与ω夹角小于90°为横向，大于90°为纵向）

4、线性可分

类似第三部分横纵向图形分类的问题就是线性可分。

线性不可分的图像数据的维度一般都很高，所以无法可视化。

二维图像也不一定线性可分（直线），比如下图

5、逻辑回归

把分类做为概率来考虑，比如前面讲到的横纵图分类问题，图像为横向的概率是80%，值设为1，图像为纵向的概率是20%，值设为0（这样设置便于处理，可以自己决定）。

5.1 sigmoid函数

在回归问题中随机梯度下降法可以使用下面的θ求出对未知数据x的输出值

$$f_θ(x) = θ^Tx$$

这里感知机的判别函数f(x)使用与回归时相同的参数θ

$$f_θ(x) = \frac{1}{1+exp(-θ^Tx)}$$

$$θ^Tx=0 {时，}f_θ(x)=0.5$$ $$0<f_θ(x)<1$$

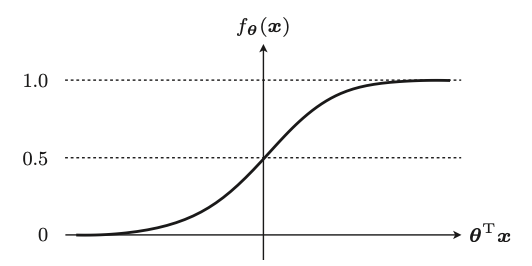
这里fθ(x)的值可以做概率。

5.2 决策边界

把未知数据x是横向图像的概率作为fθ(x)，（下面这个是条件概率，给出数据x时，图像为横向的概率）

$$P(y=1|x)= f_θ(x)$$

fθ(x)=0.2的意思图像是横向的概率是20%，纵向概率是80%，这种状态分类为纵向

我们应该把阈值设置为0.5，然后把fθ(x)的结果和它相比较

$$y= \begin{cases} 1&(\bf f_θ(x)\ge 0.5) \\ 0&(\bf f_θ(x)< 0.5) \end{cases}$$

由图可知，可以把上面的公式改成下面这种

$$y = \begin{cases} 1&(θ^T\cdot\bf x \ge 0) \newline 0&(θ^T\cdot\bf x < 0) \end{cases}$$

然后，我们像学习感知机时，设横轴为图像的宽（x1）、纵轴为图像的高（x2）

$$θ = \begin{vmatrix} θ_0 \\θ_1\\θ_2 \end{vmatrix} = \begin{vmatrix} -100 \\2\\1 \end{vmatrix} ,x= \begin{vmatrix} 1 \\x_1\\x_2 \end{vmatrix}$$

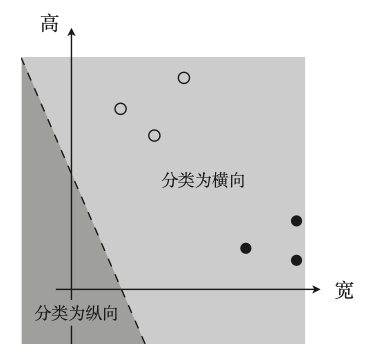
这条直线成为决策边界，

为求正确的参数θ定义目标函数，进行微分，然后求参数的更新表达式（这种算法称为逻辑回归）

6、似然函数

$$L(θ) = \prod_{i=1}^{n}P(y^{(i)}=1|x^{(i)})^{y^{(i)}}P(y^{(i)}=0|x^{(i)})^{1-y^{(i)}}$$

似然函数 L(θ) 中，使其值最大的参数 θ 能够最近似地说明训练数据。

因为连乘出来的值太小，所以可以取对数

7、对数似然函数

$$logL(θ)=log\prod_{i=1}^{n}P(y^{(i)}=1|x^{(i)})^{y^{(i)}}P(y^{(i)}=0|x^{(i)})^{1-y^{(i)}}$$

这里求更新表达式求导会有一些问题，这里直接截取关键的部分

更新表达式就会变成下面这样

$$\theta _j \mathrel{\text{:=}} \theta _j - \eta\sum _{i=1}^{n}\left( f_\theta\left( x^{(i)} \right) - y^{(i)} \right)x_j^{(i)}$$

8、线性不可分

类似下图，可以不用直线进行划分，调参可以有很好的划分效果