第1讲 神经网络计算

🖼 人工智能学习总目录

🖼 视频资料都在这里—北京大学TensorFlow2.0公开课，建议看课，这里只是我写的可参考的在线笔记

🖼 主要学会用TensorFlow2搭建神经网络方法、离散数据的分类、连续数据的预测

• 第1讲 神经网络计算
• 第2讲 神经网络优化
• 第3讲 神经网络八股
• 第4讲 网络八股扩展
• 第5讲 卷积神经网络
• 第6讲 循环神经网络

第1讲 神经网络计算，搭建出我们的第一个神经网络模型

第2讲 神经网络优化，掌握学习率、激活函数、损失函数和正则化的使用，五种反向传播优化器

第3讲 神经网络八股，用“六部分”写出手写数字模型识别训练模型

第4讲 网络八股扩展，增加自制数据集、数据增强，断点续训参数提取和acc/loss可视化，实现给图识物的应用程序

第5讲 卷积神经网络，用基础CNN、LeNet、AlexNet、VGGNet、InceptionNet、ResNet实现图像识别

第6讲 循环神经网络，用基础RNN、LSTM、GRU实现股票预测

本讲目标：了解神经网络计算过程，搭建出第一个神经网络模型。

环境：Anaconda （tersorflow虚拟环境）、Pycharm，可以看这里之前写过：Anaconda界面创建虚拟环境

# 1、创建tensorflow虚拟环境，这里没有设置python版本，会根据自己电脑下载（我觉得区别不大）
conda info --envs
conda env list
conda create --name tensorflow
conda activate tensorflow

# 2、下载tensorflow，这里没有具体设置tensorflow版本（我觉得区别不大）
conda install tensorflow

# 3、如果你是WIndwos并且有英伟达显卡，可以使用下命令配置GPU
conda install cudatoolkit = 10.1
conda install cudnn = 7.6

人工智能：让机器人具备人的思维和意识

Tensor张量：多维数组（列表），张量可以表示0~n阶数组（列表）

维数	阶	名字	例子
0-D	0	标量 scalar	s = 1
1-D	1	向量 vector	v = [ 1 , 2 , 3 ]
2-D	2	矩阵 matrix	m = [ [1,2] , [3,4] ]
n-D	n	张量 tensor	t = [[[ …

1、人工智能三学派

• 1、行为主义：基于控制论（构建感知—动作控制系统）
• 2、符号主义： 基于算术逻辑表达式（公式描述，专家系统）
• 3、连接主义：基于仿生学，模拟神经元链接（感性思维、神经网络）

我们做的主要是用计算机仿出神经连接关系（准备数据—>搭建网络—>参数优化—>应用网络）

2、神经网络设计过程

• 首先，需要准备数据，数据量越大越好，要构成特征和标签对。如要识别猫，就要有大量猫的图片和这个图片是猫的标签，构成特征标签对。

• 随后，搭建神经网络的网络结构，并通过反向传播，优化连线的权重，直到模型的识别准确率达到要求，得到最优的连线权重，把这个模型保存起来。

• 最后，用保存的模型，输入从未见过的新数据，它会通过前向传播，输出概率值，概率值最大的一个，就是分类或预测的结果。图 2.1 展示了搭建与使用神经网络模型的流程。

2.1 鸢尾花Iris数据集

输入特征：（花萼长，花萼宽，花瓣长，花瓣宽）

输出标签： 0/1/2 ， 0是狗尾草鸢尾花、1是杂色鸢尾花、2是弗吉尼亚鸢尾花

（花萼长，花萼宽，花瓣长，花瓣宽，对应类别） ——> （前四个是输入特征，最后一个是标签）

2.2 网络结构

y = x * w + b，输入一个数据x，乘自己的权值w，加上偏执b，输出y

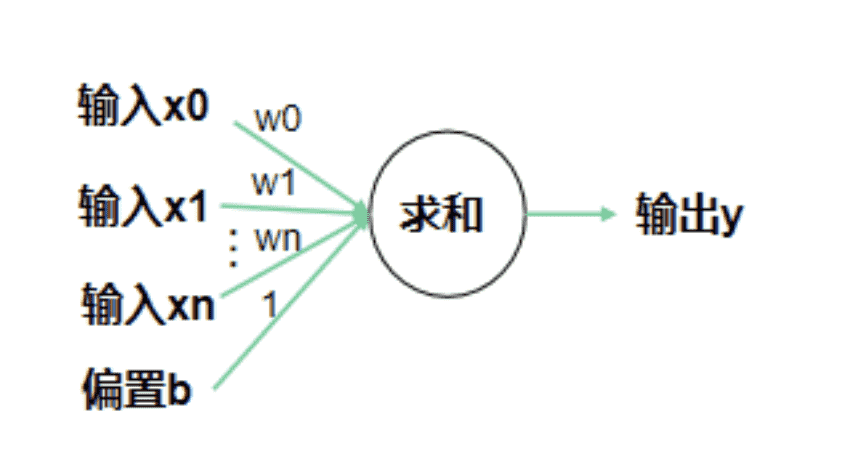
y = y0+y1+y2+y3 ， y0计算方式在上面，结果如下图有y0/y1/y2，分别对应类别0/1/2鸢尾花类型的概率

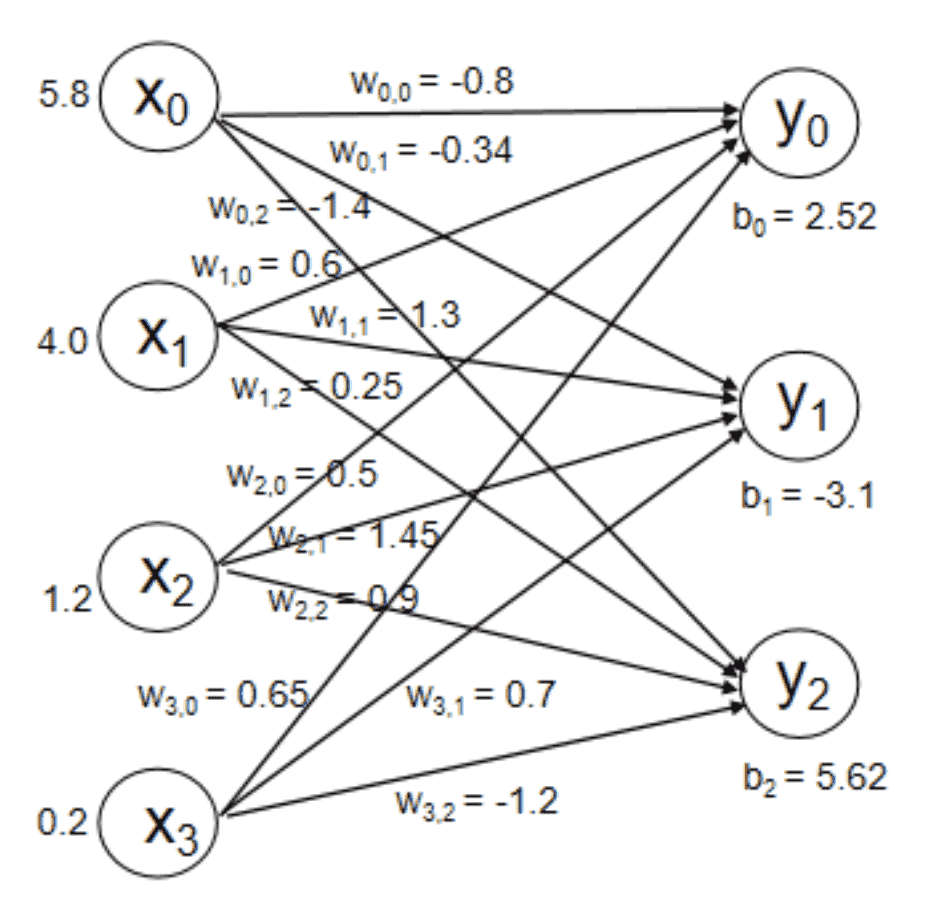
权值w和偏执b随机初始化（类似下图，4个属性x3种类型，1偏执x3种类型） —> 定量判断w、b的优劣（损失函数loss判断预测值y和标准答案y_的差距） —> 反向传播，从后向前逐层求偏导迭代参数（梯度下降法找w、b最小的值）

2.3 损失函数（loss function）

预测值（y）与标准答案（y_）的差距，一般用的是均值方差MSE(y,y_)= (y-y_)^2 /n （这里计算所有的y-y_）

2.4 梯度下降（找w、b使loss function最小）

梯度：各参数求导后的向量

梯度下降：函数减少的方向

梯度下降法：沿损失函数梯度下降的方法，寻找损失函数的最小值，得到最优参数的方法（下面公式要记住）

2.5 学习率（learning rate，lr）

简单理解成寻找损失函数最小值过程中，w、b变换的速度

学习率小，迭代过程中趋于最小值速度慢，需要多次迭代

学习率大，迭代过程中可能直接跨过最小值，找不到最优最小值点

2.6 反向传播

从后向前，逐层求偏导，迭代参数

2.7 代码示例

import tensorflow as tf

w = tf.Variable(tf.constant(5, dtype=tf.float32))
lr = 0.2
epoch = 40
# 1、for epoch 定义顶层循环，表示对数据集循环epoch次，此例数据集数据仅有1个w,初始化时候constant赋值为5，循环40次迭代。
for epoch in range(epoch):  
    # 2、with结构到grads框起了梯度的计算过程。
    with tf.GradientTape() as tape:  
        loss = tf.square(w + 1)
    # 3、.gradient函数告知谁对谁求导
    grads = tape.gradient(loss, w)  

    # 4、# .assign_sub 对变量做自减 即：w -= lr*grads 即 w = w - lr*grads
    w.assign_sub(lr * grads)  
    print("After %s epoch,w is %f,loss is %f" % (epoch, w.numpy(), loss))

# lr初始值：0.2   请自改学习率  0.001  0.999 看收敛过程
# 最终目的：找到 loss 最小 即 w = -1 的最优参数w

3、TensorFlow2.1基本概念与常见函数

import tensorflow as tf
import numpy as np

# 1、创建一个张量
a = tf.constant([1, 5], dtype=tf.int64)

# 2、把numpy转换成tensor
a = np.arange(0, 5)
b = tf.convert_to_tensor(a, dtype=tf.int64)

# 3、新建指定值填充矩阵
a = tf.zeros([2, 3])
b = tf.ones(4)
c = tf.fill([2, 2], 9)

# 4、生成正态分布随机数，下面是截断式正态分布（在μ-2σ到μ+2σ之间）
d = tf.random.normal([2, 2], mean=0.5, stddev=1)
e = tf.random.truncated_normal([2, 2], mean=0.5, stddev=1)

# 5、生成均值分布随机数
f = tf.random.uniform([2, 2], minval=0, maxval=1)

# 6、改类型，找最大最小值
x1 = tf.constant([1., 2., 3.], dtype=tf.float64)
x2 = tf.cast(x1, tf.int32)
print("minimum of x2：", tf.reduce_min(x2))
print("maxmum of x2:", tf.reduce_max(x2))

# 7、求均值、求和，这里axis可以控制维度（axis=0是以列为单位，axis=1是以行为单位）
x = tf.constant([[1, 2, 3], [2, 2, 3]])
print("mean of x:", tf.reduce_mean(x))  # 求x中所有数的均值
print("sum of x:", tf.reduce_sum(x, axis=1))  # 求每一行的和

# 8、 加减乘除
a = tf.ones([1, 3])
b = tf.fill([1, 3], 3.)
print("a+b:", tf.add(a, b))
print("a-b:", tf.subtract(a, b))
print("a*b:", tf.multiply(a, b))
print("b/a:", tf.divide(b, a))

# 9、平方、n次方、开方
a = tf.fill([1, 2], 3.)
print("a的平方:", tf.square(a))
print("a的3次方:", tf.pow(a, 3))
print("a的开方:", tf.sqrt(a))

# 10、矩阵乘，(3,2) * (2,3) = 3x3的矩阵
a = tf.ones([3, 2])
b = tf.fill([2, 3], 3.)
print("a*b:", tf.matmul(a, b))

# 11、将变量标记为可训练（被标记的变量会在反向传播中记录梯度信息）,下面这个w是随机权值例子
w = tf.Variable(tf.random.normal([2,2],mean=0,stddev=1))

# 12、组合输入特征和标签
features = tf.constant([12, 23, 10, 17])
labels = tf.constant([0, 1, 1, 0])
dataset = tf.data.Dataset.from_tensor_slices((features, labels))
for element in dataset:
    print(element)

# 13、求张量梯度，with结构记录计算过程，gradient求出张量的梯度
with tf.GradientTape() as tape:
    x = tf.Variable(tf.constant(3.0))
    y = tf.pow(x, 2)
grad = tape.gradient(y, x)
print(grad)

# 14、根据索引和元素，索引列表
seq = ['one', 'two', 'three']
for i, element in enumerate(seq):
    print(i, element)

# 15、one-hot encoding独热编码，分类问题常用，1表示是，0表示非
classes = 3
labels = tf.constant([1, 0, 2])  # 输入的元素值最小为0，最大为2
# labels 表示待转换的数据，depth表示有几个分类
output = tf.one_hot(labels, depth=classes)
print("result of labels1:", output)

# 16、使输出符合概率分布 e^y1 /( e^y1 + e^y2 + e^y3)，之后的p1+p2+p3=1
y = tf.constant([1.01, 2.01, -0.66])
y_pro = tf.nn.softmax(y)
print("After softmax, y_pro is:", y_pro)  # y_pro 符合概率分布
print("The sum of y_pro:", tf.reduce_sum(y_pro))  # 通过softmax后，所有概率加起来和为1

# 17、assign_sub自减函数
x = tf.Variable(4)
x.assign_sub(1) # x每次自减1
print("x:", x)  # 4-1=3

# 18、返回指定操作轴最大值的索引号
test = np.array([[1, 2, 3], [2, 3, 4], [5, 4, 3], [8, 7, 2]])
print("每一列的最大值的索引：", tf.argmax(test, axis=0))  # 返回每一列最大值的索引
print("每一行的最大值的索引", tf.argmax(test, axis=1))  # 返回每一行最大值的索引
 

4、鸢尾花数据集

4.1 加载鸢尾花数据集

# 这里下载的是包的命令是conda install scikit-learn，不是sklearn包
from sklearn import datasets
from pandas import DataFrame
import pandas as pd

x_data = datasets.load_iris().data  # .data返回iris数据集所有输入特征
y_data = datasets.load_iris().target  # .target返回iris数据集所有标签
print("x_data from datasets: \n", x_data)
print("y_data from datasets: \n", y_data)

x_data = DataFrame(x_data, columns=['花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度']) # 为表格增加行索引（左侧）和列标签（上方）
pd.set_option('display.unicode.east_asian_width', True)  # 设置列名对齐
print("x_data add index: \n", x_data)

x_data['类别'] = y_data  # 新加一列，列标签为‘类别’，数据为y_data
print("x_data add a column: \n", x_data)

#类型维度不确定时，建议用print函数打印出来确认效果

4.2 实现鸢尾花分类

下面这段代码很重要，希望你可以背下来

1、准备数据

• 数据集读入
• 数据集乱序
• 生成训练集和测试集（x_train、y_train和x_test、y_test）
• 配对（输入特征，标签），每次读入一小撮（batch）

2、搭建神经网络

• 定义神经网络中所有可训练的参数

3、参数优化

• 嵌套循环迭代，with结构更新参数，显示当前loss

4、测试效果

• 计算当前参数前行传播后的准确率，显示当前acc

5、acc/loss可视化

# 利用鸢尾花数据集，实现前向传播、反向传播，可视化loss曲线

# 导入所需模块
import tensorflow as tf
from sklearn import datasets
from matplotlib import pyplot as plt
import numpy as np

# 1、导入数据，分别为输入特征和标签
x_data = datasets.load_iris().data
y_data = datasets.load_iris().target

# 随机打乱数据（因为原始数据是顺序的，顺序不打乱会影响准确率）
# seed: 随机数种子，是一个整数，当设置之后，每次生成的随机数都一样（为方便教学，以保每位同学结果一致）
np.random.seed(116)  # 使用相同的seed，保证输入特征和标签一一对应
np.random.shuffle(x_data)
np.random.seed(116)
np.random.shuffle(y_data)
tf.random.set_seed(116)

# 将打乱后的数据集分割为训练集和测试集，训练集为前120行，测试集为后30行
x_train = x_data[:-30]
y_train = y_data[:-30]
x_test = x_data[-30:]
y_test = y_data[-30:]

# 转换x的数据类型，否则后面矩阵相乘时会因数据类型不一致报错
x_train = tf.cast(x_train, tf.float32)
x_test = tf.cast(x_test, tf.float32)

# from_tensor_slices函数使输入特征和标签值一一对应。（把数据集分批次，32个为一组，每个批次batch组数据）
train_db = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(32)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(32)

# 2、生成神经网络的参数，4个输入特征故，输入层为4个输入节点；因为3分类，故输出层为3个神经元
# 用tf.Variable()标记参数可训练
# 使用seed使每次生成的随机数相同（方便教学，使大家结果都一致，在现实使用时不写seed）
w1 = tf.Variable(tf.random.truncated_normal([4, 3], stddev=0.1, seed=1))
b1 = tf.Variable(tf.random.truncated_normal([3], stddev=0.1, seed=1))

lr = 0.1  # 学习率为0.1
train_loss_results = []  # 将每轮的loss记录在此列表中，为后续画loss曲线提供数据
test_acc = []  # 将每轮的acc记录在此列表中，为后续画acc曲线提供数据
epoch = 500  # 循环500轮
loss_all = 0  # 每轮分4个step，loss_all记录四个step生成的4个loss的和

# 训练部分
for epoch in range(epoch):  #数据集级别的循环，每个epoch循环一次数据集
    for step, (x_train, y_train) in enumerate(train_db):  #batch级别的循环 ，每个step循环一个batch
        with tf.GradientTape() as tape:  # with结构记录梯度信息
            y = tf.matmul(x_train, w1) + b1  # 神经网络乘加运算
            y = tf.nn.softmax(y)  # 使输出y符合概率分布（此操作后与独热码同量级，可相减求loss）
            y_ = tf.one_hot(y_train, depth=3)  # 将标签值转换为独热码格式，方便计算loss和accuracy
            loss = tf.reduce_mean(tf.square(y_ - y))  # 采用均方误差损失函数mse = mean(sum(y-out)^2)
            loss_all += loss.numpy()  # 将每个step计算出的loss累加，为后续求loss平均值提供数据，这样计算的loss更准确
        # 计算loss对各个参数的梯度
        grads = tape.gradient(loss, [w1, b1])

        # 实现梯度更新 w1 = w1 - lr * w1_grad    b = b - lr * b_grad
        w1.assign_sub(lr * grads[0])  # 参数w1自更新
        b1.assign_sub(lr * grads[1])  # 参数b自更新

    # 每个epoch，打印loss信息
    print("Epoch {}, loss: {}".format(epoch, loss_all/4))
    train_loss_results.append(loss_all / 4)  # 将4个step的loss求平均记录在此变量中
    loss_all = 0  # loss_all归零，为记录下一个epoch的loss做准备

    # 测试部分
    # total_correct为预测对的样本个数, total_number为测试的总样本数，将这两个变量都初始化为0
    total_correct, total_number = 0, 0
    for x_test, y_test in test_db:
        # 使用更新后的参数进行预测
        y = tf.matmul(x_test, w1) + b1
        y = tf.nn.softmax(y)
        pred = tf.argmax(y, axis=1)  # 返回y中最大值的索引，即预测的分类
        # 将pred转换为y_test的数据类型
        pred = tf.cast(pred, dtype=y_test.dtype)
        # 若分类正确，则correct=1，否则为0，将bool型的结果转换为int型
        correct = tf.cast(tf.equal(pred, y_test), dtype=tf.int32)
        # 将每个batch的correct数加起来
        correct = tf.reduce_sum(correct)
        # 将所有batch中的correct数加起来
        total_correct += int(correct)
        # total_number为测试的总样本数，也就是x_test的行数，shape[0]返回变量的行数
        total_number += x_test.shape[0]
    # 总的准确率等于total_correct/total_number
    acc = total_correct / total_number
    test_acc.append(acc)
    print("Test_acc:", acc)
    print("--------------------------")

# 绘制 loss 曲线
plt.title('Loss Function Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Loss')  # y轴变量名称
plt.plot(train_loss_results, label="$Loss$")  # 逐点画出trian_loss_results值并连线，连线图标是Loss
plt.legend()  # 画出曲线图标
plt.show()  # 画出图像

# 绘制 Accuracy 曲线
plt.title('Acc Curve')  # 图片标题
plt.xlabel('Epoch')  # x轴变量名称
plt.ylabel('Acc')  # y轴变量名称
plt.plot(test_acc, label="$Accuracy$")  # 逐点画出test_acc值并连线，连线图标是Accuracy
plt.legend()
plt.show()